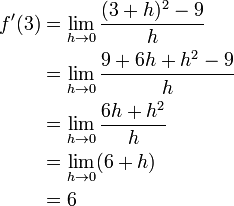Berikut ini daftar Lowongan Kerja Resmi kalkulus Terbaru November 2014 dari Situs Lowongan Kerja Resmi, Semoga Lowongan Kerja Resmi kalkulus Terbaru November 2014 ini bermanfaat bagi anda.

SOAL JAWAB UAS GANJIL TH. 2011 - 2012 November 2014

                    SOAL UJIAN AKHIR SEMESTER GANJIL TH. 2011 - 2012

===========================================================
Mata Kuliyah           : KALKULUS 1                                   Sifat           : Tutup Buku
Jam                              : 07.30 - 09.10 WIB                         Waktu       : 100 Menit
Hari / Tanggal        : Jum'at / 13 Jan 2011                                             
Kelompok                 :- A11-4101                                           Dosen       : Tim Dosen Pengampu
                                        - A11-4103 s/d A11-4112
                                        - A11-4116 s/d A11-4118
===========================================================

1. Tentukan Nilai Maksimum dari Fungsi f(x)= (2 + x2 )(2x +1)-1?
     Jawab :
     Cari Titik kritisnya :
     a. Turunkan fungsi f(x) menjadi f '(x)= 0, dengan rumus turunan :
         * f '(x) = (u'v - uv').v-2
           Jadi misal : u = 2 + x2      &       v = 2x +1
                                 u' = 2x                    v' = 2


     b. Substitusikan ke rumus turunannya :
            f '(x) = (u'v - uv').v-2
            f '(x) = (2x(2x+1) - (2 + x2 )2) (2x +1)-2
            f '(x) = (2x + 4x2-4 - 2x2) (2x +1)-2
            f '(x) = 2 (x + 2) (x - 1) (2x +1)-2
     c. Cari nilai x penghasil f '(x)= 0.
        f '(x) = 2 (x + 2) (x - 1) (2x +1)-2
              x = -2 || x = 1 || x = -1/2

     d. Substitusikan nilai x ke fungsi f(x) dan cari nilai Minimum dan Maximumnya.
        x = -2, 
           f (-2) = (2 + (-2)2 )(2(-2) +1)-1 
                     =  (2 + 4)/-3 = -2
        x = 1,
           f (1) = (2 + (1)2 )(2(1) +1)-1 
                   =  (2 + 1)/3 = 1
        x = -1/2, 
           f (-1/2) = (2 + (-1/2)2 )(2(-1/2) +1)-1 
                          =  (2 + 4)/0 =0
        Jadi, 
              * Nilai Maksimum : 1   pada x = 1
              * Nilai Minimum    : -2 pada x = -2

2. Diketahui fungsi  f(x)= x4 - 4x3 + 4x2 + 2
    Tentukan :
    a. Titik Stasioner atau Titik Kritisnya
    b. Interval dimana f(x) NAIK dan interval dimana f(x) TURUN
    c. Gambarkan Sketsa Grafiknya 
    Jawab :
       a. Titik Stasioner dan Titik Kritis.
          1. Turunkan fungsi f(x) menjadi f '(x)= 0, dengan rumus turunan.
          2. Cari nilai x dari f '(x)
              f '(x) = 4x3 + 12x2 + 8x = 4x(x2- 3x + 2)
              4x(x - 1)(x -2) = 0
              x = 0 || x = 1 || x = 2
              Titik kritisnya : 0, 1, 2
          3. Substitusikan nilai x ke f(x)
             x = 0,
                    f(0)= (0)4 - 4.(0)3 + 4.(0)2 + 2 = 2
             x =1,
                    f(1)= (1)4 - 4(1)3 + 4(1)2 + 2  = 3
             x = 2,
                   f(2)= (2)4 - 4(2)3 + 4(2)2 + 2  = 2
            Titik Stasioner : [2,2] 
      b. Interval f(x) Naik da Turun.
          Titik kritis : 0, 1, 2
                                                -            +             -             +
                                           ______|_______|_______|_______
                                                      0             1             2
          1. Naik f '(x) > 0 
              Intervalnya adalah (1 > x > 0 dan x > 2)
          2. Turun f '(x) < 0 
              Intervalnya adalah ( x < 0 dan 1< x <2)
     c. Grafik
                    3 |      *
                        |           
                    2 | *         *
                        |
                  - 1 |   +    -     +
         _____|___,___,________
                       |0    1     2
                       |

                                             
3. Pak Tani punya rencana akan beternak itik, menurut aturan 1 m2 luas kandang harus
    ditempati 50 ekor itik, pak Tani mempunyai kawat yang bisa dibuat kandang itik
    panjangnya 30 meter, dibelakang rumah pak Tani ada tembok, kandang itik yang
    akan dibuat bentuknya segiempat, salah satu sisi kandang adalah tembok dan
    ketiga sisi yang lain adalah kawat, Anda sebagai mahasiswa Udinus yang sudah belajar
    kalkulus, coba beri solusi berapa ukuran kandang yang harus dibuat pak Tani agar
    dapat memuat itik semaksimal mungkin dan berapa ekor itik yang harus 
    dibeli pak tani?
    Jawab :
                            tembok
                         _________
                        |                      |                 *  inisialisasi  :
       kawatX  |                       |    kawatX              kawatX = x
                        | ________|                                 kawatY = y
                           kawatY
 
    Jadi :
              2x + y = 30 ,  y = 30 - 2x
    L = x . y
       = x . (30 - 2x)
       = 30x - 2x2 
         
     L ' = 0
     L ' = 30 - 4x
      x = 30/4 ,
      y = 30 - 2x
      y = 30 - 2(30/4)
      y = 30 - 15 = 15

    L maks = x . y                         Jumlah Itik = Lmaks x 50
             = 30/4 x 15                                  = 112,5 x 50
             =7,5 x 15                                       = 5625 ekor itik
             =112,5 m2

4. Tentukan :
     a. Integral dari (x+2)(x3-5x2+4x)-1dx
     b. Integral dari (4x+8)(x2+4x) dx dengan interval [0,1]?

5. Tentukan Luas yang dibatasi oleh fungsi :
      
                         1- x2    jika 0<= x <= 2
       f(x)= -3  jika 2 <= x <=3
               6-x   jika 3 <= x <= 7

6. Diketahui volume benda putar yang dibatasi fungsi f(x)= 2 - 2x dalam interval [-2,0]
   diputar mengelililngi sumbu-x sejauh 3600 ??


* SELAMAT MENGERJAKAN  *

SOAL JAWAB UAS GANJIL TH. 2010 - 2011 November 2014

                    SOAL UJIAN AKHIR SEMESTER GANJIL TH. 2010 - 2011

===========================================================
Mata Kuliyah           : KALKULUS 1                                   Sifat           : Tutup Buku
Jam                              : 07.30 - 09.10 WIB                         Waktu       : 100 Menit
Hari / Tanggal        : Jum'at / 14 Jan 2011                                             
Kelompok                : A11-4101 s/d A11-4112                 Dosen       : Tim Dosen Pengampu
===========================================================

1. Tentukan Nilai Maksimum dari Fungsi f(x)= (2 + x2 )(2x +1)-1?

2. Diketahui fungsi  f(x)= x4 - 4x3 + 4x2 + 2
    Tentukan :
    a. Titik Stasioner atau Titik Kritisnya
    b. Interval dimana f(x) NAIK dan interval dimana f(x) TURUN
    c. Gambarkan Sketsa Grafiknya

3. Pak Tani Mempunyai Kawat panjangnya 100 meter, kawat tersebut akan di gunakan
    untuk membuat kandang itik yang bentuknya segiempat, karena di belakang rumah 
    pak Tani ada tembok, maka salah salah satu sisi lainnya dari kawat, jika dalam 1 m2
    dapat memuat 50 ekor itik, maka pak tani dapat memelihara paling banyak
    berapa ekor itik ?

4. Tentukan integral dari (x+2)(x3-5x2+4x)-1dx ?

5. Tentukan :
    a. Diketahui daerah A di batasi oleh dua fungsi yaitu, f(x)= x2 - 4 dan g(x)= 2x - x2 
        serta interval [-2,1],
        Tentukan luas daerah A tersebut.
    b. Daerah A dibatasi oleh fungsi berikut :
      
                         1     jika -1<= x <= 0
       f(x)= 1-x  jika 0 <= x <= 2
               -1   jika 2 <= x <= 3

       Tentukan Luas daerah A?

6. Diketahui daerah A dibatasi oleh fungsi f(x)= 2 - 2x dalam interval [-2,0] diputar
    mengelililngi sumbu-x sejauh 3600 Tentukan benda apa yang terbentuk ?
    dan berapa volumenya.


* SELAMAT MENGERJAKAN  *

Integral dan Turunan November 2014

A. Turunan


Grafik Fungsi Turunan
Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.
Secara matematis, turunan fungsi ƒ(x) terhadap variabel x adalah ƒ′ yang nilainya pada titik x adalah:
f'(x)=\lim_{h \to 0}{f(x+h) - f(x)\over{h}} ,
dengan syarat limit tersebut eksis. Jika ƒ′ eksis pada titik x tertentu, kita katakan bahwa ƒ terdiferensialkan (memiliki turunan) pada x, dan jika ƒ′ eksis di setiap titik pada domain ƒ, kita sebut ƒ terdiferensialkan.
Apabila z = x + h, h = x - z, dan h mendekati 0 jika dan hanya jika z mendekati x, maka definisi turunan di atas dapat pula kita tulis sebagai:
Garis singgung pada (x, f(x)).
f'(x)=\lim_{z \to x}{f(z) - f(x)\over{z-x}}

Turunan f'(x) sebuah kurva pada sebuah titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut.
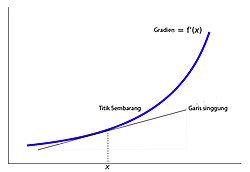
Perhatikan bahwa ekspresi {f(x+h) - f(x)\over{h}} pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
Sebagai contoh, untuk menemukan gradien dari fungsi f(x) = x2 pada titik (3,9):



\begin{align} f'(3)&=\lim_{h \to 0}{(3+h)^2 - 9\over{h}} \\ &=\lim_{h \to 0}{9 + 6h + h^2 - 9\over{h}} \\ &=\lim_{h \to 0}{6h + h^2\over{h}} \\ &=\lim_{h \to 0} (6 + h) \\ &= 6 \end{align}

Read more »
Home/Lowongan kalkulus